Investigating the properties of Quark-Gluon Plasma with nontrivial collective phenomena and correlation technique
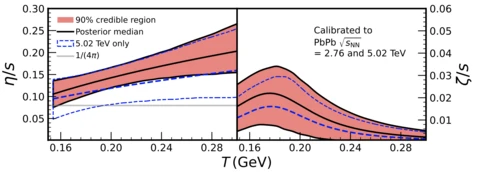
significantly obtained by including higher-order νn observables in Bayesian studies. Figure taken from e-Print: 2111.08145.
Nearly 14 billion years ago, our Universe burst into existence in the Big Bang. In the first few microseconds after the Big Bang, it is believed that the Universe was filled with Quark-Gluon Plasma. This extreme state of nuclear matter consists of deconfined quarks and gluons, interacting dominantly via the strong nuclear force, one of the four fundamental forces in nature. The Quark-Gluon Plasma does not exist at ordinary temperatures and energy densities, where the building blocks of matter are composite particles, baryons (made up of three quarks) and mesons (made up of one quark and one antiquark). Closely related to this is the so-called asymptotic freedom, which states that quarks interact weakly at large energies (or, equivalently, at short distances). As the distance between quarks in composite particles increases, their interaction energy increases as well, which prevents the quarks from being separated. In collisions of heavy ions at the Large Hadron Collider, the Quark-Gluon Plasma can be produced. Therefore, by producing and studying the properties of Quark-Gluon Plasma in heavy-ion collisions at the Large Hadron Collider, we are essentially recreating and studying the conditions that existed in the distant past of our Universe and shedding light on its evolution.
In non-central heavy-ion collisions, the initial ellipsoidal volume containing the interacting nuclear matter is anisotropic in the coordinate space, due to the geometry of non-central collisions. Multiple interactions
within this anisotropic volume cause the anisotropy to be transferred from the coordinate space into the momentum space. In essence, this transfer is the anisotropic flow phenomenon. The resulting anisotropy in
momentum space will cause an anisotropic distribution of particles recorded in the detector after each heavy-ion collision, and is therefore an observable quantity. The occurrence of large anisotropic flow in heavy-ion collisions demonstrated that the Quark-Gluon Plasma behaves like a strongly coupled liquid with a very small ratio of shear viscosity to entropy density, which is very close to a universal lower bound of 1⁄4pi obtained from theoretical arguments based on the AdS/CFT conjecture (the fundamental duality between general relativity and conformal field theory).
Anisotropic flow degrees of freedom, amplitudes νn and symmetry planes Ψn, cannot be measured directly in an experiment - instead, they are estimated with multiparticle azimuthal correlations, which are obtained directly from reconstructed azimuthal angles of produced particles. To suppress systematic biases, improved estimators are obtained using multivariate cumulants instead of multiparticle correlations. In addition, each multivariate cumulant by definition carries a piece of independent information about the properties of the Quark-Gluon Plasma. Establishing such a new set of independent observables is particularly important in the context of currently ongoing state-of-the-art Bayesian studies, which act as a bridge between experiment and theory.