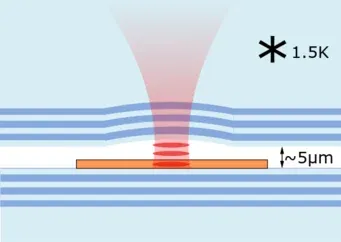
Our group follows two different approaches to realize quantum networks with individual Erbium ions. The first approach uses Fabry-Perot resonators (see figure). To achieve the highest possible reduction of the excited state lifetime, we have assembled resonators with the smallest possible mode volume and the highest possible quality factor, as summarized here.
To achieve these goals, we use mirrors with a spherical depression of about 150 µm radius of curvature, which we have fabricated by laser ablation. With commercially available dielectric coatings, we observe a Finesse of 105. This means that every photon will bounce between the mirrors 30 000 times before leaving the resonator! Thus, the interaction probability with single Erbium ions, embedded in a thin membrane in the resonator, is maximized. To fabricate these membranes, we have implemented a polishing technique that gives us 10 – 20 micrometer thin membranes of crystalline Yttrium Orthosilicate with a surface roughness below 0.3 nm rms. This is almost atomically flat, which minimizes scattering und thus unwanted photon loss.
To use the resulting narrow-linewidth resonator, it needs to be tuned and stabilized to the emission frequency of the Erbium ions. This requires us to control the distance between the mirrors with a precision of about one picometer (on average). This is much less than the size of a single atom! We have recently achieved this challenging requirement and are currently working towards the spectroscopy and control of individual ions. We expect to reduce the lifetime of Erbium ions in our resonator by a factor of 100. This means that the implementation of large-scale quantum networks will not be limited by the time it takes to generate a photon, but by the time it takes to transmit it to a remote receiver, which constitutes a critical milestone for our efforts.
In addition, we plan to control multiple erbium dopants in the same resonator by frequency-domain multiplexing. Recently, we have investigated if spin-spin interactions will limit the coherence time in this approach. The results can be found in: Merkel, Cova Fariña, and Reiserer: Dynamical decoupling of spin ensembles with strong anisotropic interactions, Phys.Rev.Lett. 127 (2021). arXiv:2005.08822 (2020).