Studying coupled oscillators is intriguing due to the emergence of self-organized collective behaviors such as synchronization and pattern formation. Analyzing the dynamics of these systems provides insights into fundamental principles governing complex phenomena in diverse fields, including physics, engineering, biology, and social sciences. While our research group has investigated diverse systems of coupled oscillators, two systems stand out:
- Globally coupled amplitude oscillators
- Coupled populations of phase oscillators
The first project originates from the attempt to describe the emergent spatiotemporal results of an electrochemical experiment.
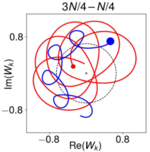
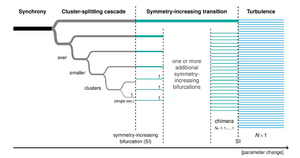
Using globally coupled Stuart-Landau oscillators, we focus our interest on the transition from coherence to spatiotemporal turbulence where we explore a range of coexisting patterns such as synchronous solutions, clustering solutions, chimera states, and incoherent solutions. Our main analysis tools are numerical integration experiments, bifurcation analysis, and symmetry arguments.
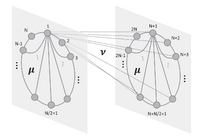
The second project dives into the study of populations of diverse phase oscillators with different inter- and intra-population coupling. Here we explore a wide range of system topologies and geometries as well as global and nonlocal coupling. We use dimension-reducing approaches as well as different theoretical methods.
Recent publications
- S. Lee, Y. Jeong, S. Son and K. Krischer
Volcano transition in a system of generalized Kuramoto oscillators with random frustrated interactions
J. Phys. A: Math. Theor. 57 085702 (2024)
- S. Lee and K. Krischer
Chimera dynamics of generalized Kuramoto-Sakaguchi oscillators in two-population networks
J. Phys. A: Math. Theor. 56 405001 (2023)
- S. Lee and K. Krischer
Heteroclinic switching between chimeras in a ring of six oscillator populations
Chaos 33, 063120 (2023)
- S. Lee and K. Krischer
Chaotic chimera attractors in a triangular network of identical oscillators
Phys. Rev. E 107, 054205
- V. G. Morales, J. A.Manzanares, and K. Krischer
Chimera states under genuine local coupling
Chaos, Solitons and Fractals 165 (2022) 112808
- S. Lee and K. Krischer
Nontrivial twisted states in nonlocally coupled Stuart-Landau oscillator
Phys. Rev. E 106, 044210
- M. Salman,C. Bick, and K. Krischer
Bifurcations of Clusters and Collective Oscillations in Networks of Bistable Units
Chaos 31, 113140 (2021)
- S. Lee and K. Krischer
Attracting Poisson chimeras in two-population networks
Chaos 31, 113101 (2021)
- S.W. Haugland, A. Tosolini, and K. Krischer
Between synchrony and turbulence: Intricate hierarchies of coexistence patterns
Nature Communications, 12:5634 (2021)
- Juliane C. Wiehl, Maximilian Patzauer and Katharina Krischer
Birhythmicity, intrinsic entrainment, and minimal chimeras in an electrochemical experiment
Chaos 31, 091102 (2021)
- F.P. Kemeth, B. Fiedler, S.W. Haugland, and K. Krischer
2-Cluster fixed-point analysis of mean-coupled Stuart-Landau oscillators in the center manifold
J. Phys. Complex. 2, 025005 (2021)
- B. Fiedler, F.P. Kemeth, S.W. Haugland,K. Krischer
Global heteroclinic rebel dynamics among large 2-Cclusters in permutation equivariant systems
SIAM Journal on Applied Dynamical Systems 20, 1277 - 1319 (2021)