Biomagnetical Signal Modeling & Reconstruction
Overview
This research focuses on the modeling, analysis, and reconstruction of cardiac magnetic signals measured with optically pumped magnetometers in magnetocardiography (MCG) and fetal MCG (fMCG).
We combine multichannel signal decomposition, forward electromagnetic modeling, and inverse reconstruction methods to extract the cardiac source dynamics with high spatial and temporal precision.
These approaches are not only essential for clinical applications, but also provide powerful tools transferable to fundamental precision experiments — such as 4π magnetic field reconstructions in spin-precession setups.
Signal Separation in Multichannel MCG Data
Multichannel MCG and fMCG recordings contain overlapping signals from maternal and fetal hearts, environmental noise, and instrumental artefacts.
To extract the relevant sources, Independent Component Analysis (ICA) and other blind-source separation methods are applied.
The workflow typically involves:
- Preprocessing through filtering and normalization,
- ICA-based decomposition to identify statistically independent components,
- and postprocessing to reconstruct or subtract noise contributions.
Time-adaptive ICA approaches enable the analysis of moving or varying sources, allowing the separation of cardiac signals even in the presence of motion or low SNR.
These methods are quantitatively evaluated using objective performance metrics, and form the foundation for subsequent modeling and reconstruction steps.
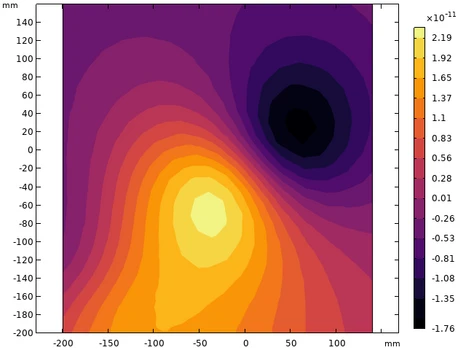
Forward Modeling of the Cardiac Magnetic Field
To understand and predict the magnetic field generated by the heart, a forward model based on the Bidomain representation of cardiac tissue is implemented.
In this model, the intracellular and extracellular spaces are treated as coupled conductive media, and the resulting current and potential distributions are computed numerically.
The simulations are performed using finite element methods (FEM), where the governing electromagnetic and electrophysiological equations—including the quasistatic form of Maxwell’s equations and the transmembrane current continuity relations—are implemented directly.
This framework allows for the inclusion of:
- anisotropic tissue conductivities,
- layered geometries representing the thorax and maternal tissues,
- adaptation of the model to patents or specific pathologies.
The computed field maps serve both as validation for experimental data and as a reference for evaluating the performance of different reconstruction methods
Inverse Reconstruction of Cardiac Sources
The inverse problem—determining the internal cardiac current distributions from the measured magnetic fields—is mathematically challenging due to its ill-posed nature and high sensitivity to noise.
While traditional approaches rely on simplified models such as equivalent current dipoles, newer techniques explore Physics-Informed Neural Networks (PINNs) to reconstruct the underlying current patterns.
Unlike purely data-driven neural networks, PINNs embed the physical laws governing electromagnetic fields directly into their training process.
This means that instead of learning arbitrary correlations, the network must produce solutions that simultaneously satisfy:
- the measured magnetic data, and
- the differential equations describing the magnetic field and current continuity.
The result is a model that can generalize beyond the training data, remain stable under noise, and adapt to complex geometries or boundary conditions.
In MCG, this allows the reconstruction of spatially resolved current densities and activation patterns that are consistent with both experimental data and physical principles.
The same framework can later be transferred to precision field reconstructions in fundamental experiments, such as spin-precession setups, where it supports 4π magnetic field mapping and systematic error analysis.
Contact
For collaboration, thesis opportunities, or further inquiries, please contact:
M.Sc. Philipp Wunderl
- Tel.: +49 (89) 289 - 51327, 53716
- Raum: 5117.02.304
- philipp.wunderl@tum.de
Publications and finished Theses
Involved Persons and Former Members
Currently Involved persons: Philipp Wunderl, Lena Wunderl, Chiara Weckmann
Former Members: