Skip to content
Technical University of Munich

Bosonic and Fermionic Impurity Models in Circuit QED

Waveguide QED with interacting photons. Two-levels emitters (in orange), realized by highly non-linear superconducting circuits, are linked via a waveguide (blue), modelled by a chain of capacitively coupled superconducting circuits. The anharmonicity of the latter induces interaction between the photons propagating in the waveguide.
Ground state phases of the bosonic impurity model with 4 excitations per unit-cell. (a) Average photon number of a cavity coupled to a qubit. The number of bound photons depends on the photon-photon interaction U and cavity-atom coupling g. (b) Long-range correlations between the atoms appearing near the transition lines between the different multi-photon bound phases. (c) In green, orange, red, algebraic decay of the atom-atom correlations on the transition lines. In blue, exponential decay of the correlations in the insulating phases.

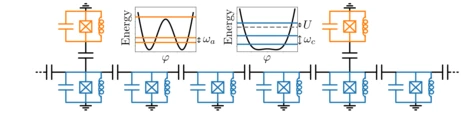
Superconducting quantum circuits offer a powerful platform for analog quantum simulation of many-body physics. One-dimensional arrays of superconducting resonators can naturally emulate bosonic Hamiltonians, where nonlinear circuit elements introduce photon–photon interactions. Using the Jordan–Wigner transformation, even fermionic models-such as those relevant to electronic systems-can be mapped onto these bosonic platforms, enabling the exploration of impurity physics in both regimes.

We have theoretically studied impurity models implemented in waveguide-QED architectures, where qubits act as artificial atoms coupled to chains of weakly nonlinear resonators. Our analysis reveals how competition between photon–photon and atom–photon interactions gives rise to distinct multi-photon bound states and correlated phases. At the phase boundaries, long-range correlations emerge, suggesting rich many-body behavior that can be probed in current experiments.

We also propose a circuit-QED realization of the Kondo impurity problem, where fermionic interactions are mapped to cross-Kerr couplings between superconducting modes. This approach reproduces the formation of the Kondo singlet, a hallmark of many-body quantum correlations, through measurable spin-spin correlations in the simulated system.

 

People: Adrian Misselwitz, Jacquelin Luneau

To top